# Fit의 과정

전체 구조가 self._init_centeroids -> kmeans_single -> 데이터 검증 후 갱신을 반복함
# kmeans_single

따라서 분기문에 따르면 _kmeans_single_elkan이라는 함수를 찾으면 됨
# _kmeans_single_elkan_1
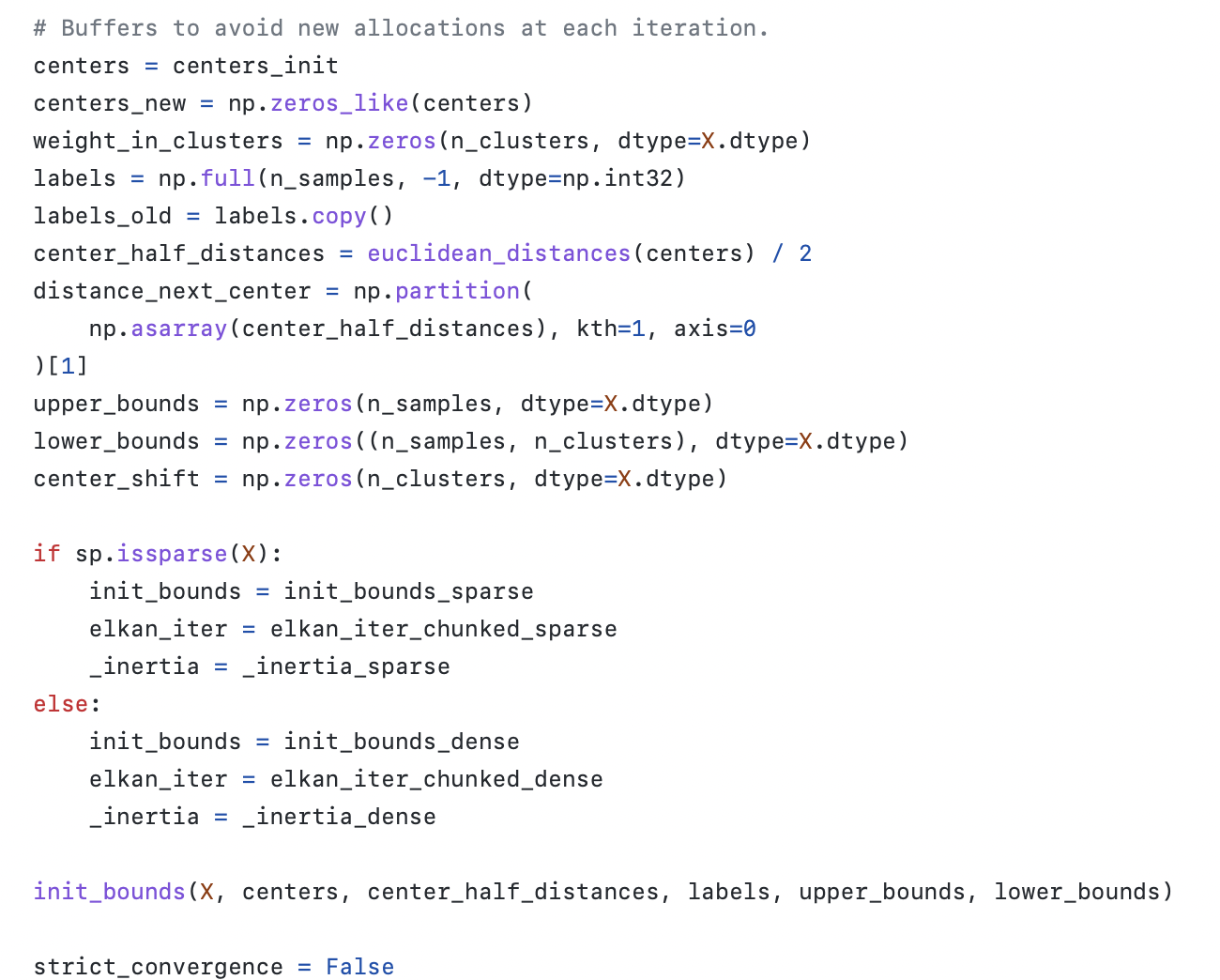
매번 다른 할당을 피하기 위해 처음부터 변수 초기화 부터 함 centers, centers_new, weight_in_clusters, labels, labels_old, center_half_distances, distance_next_center, upper_bounds, lower_bounds, strict_convergence
분기문에 따라 elkan_iter는 elkan_iter_chunked_dense라고 보면 됨
# _kmeans_single_elkan_2


전체적 구조는 centers, centers_new, inertia, strict_convergence 등 변수를 계산하고 갱신하는 것을 반복하는 과정
strict_convergence : 센터가 수렴할때 True, 수렴하지 않을때 False
strict_convergence가 False일때 반복문 진행, True일때 break 하고 반복문 나감
이때 strict_convergence가 수렴하는지의 여부는 np.array_equal함수로 array객체간의 비교와 tol 값과 center_shift의 제곱의 합간의 비교에 의해 판단.
tol = 1e-4라는 상수라고 생각하면 됨
center_shift는 이전 센터와 현재 갱신된 센터간의 거리라고 보면 됨. 즉, 센터의 변화가 어떤 상수값보다 크면 반복문 진행, 작으면 반복문 중단.
[K-means 출처]
https://github.com/scikit-learn/scikit-learn/blob/main/sklearn/cluster/_kmeans.pyhttps://github.com/scikit-learn/scikit-learn/blob/main/sklearn/cluster/_k_means_elkan.pyx
https://github.com/scikit-learn/scikit-learn/blob/main/sklearn/cluster/_k_means_elkan.pyx
아래의 코드 리뷰는 나중에 할 예정
cls = AgglomerativeClustering(n_clusters = 3)
1. Kmeans
| def __init__( | |
| self, | |
| n_clusters=8, | |
| *, | |
| init="k-means++", | |
| n_init=10, | |
| max_iter=300, | |
| tol=1e-4, | |
| verbose=0, | |
| random_state=None, | |
| copy_x=True, | |
| algorithm="auto", | |
| ): | |
| self.n_clusters = n_clusters | |
| self.init = init | |
| self.max_iter = max_iter | |
| self.tol = tol | |
| self.n_init = n_init | |
| self.verbose = verbose | |
| self.random_state = random_state | |
| self.copy_x = copy_x | |
| self.algorithm = algorithm | |
self.n_clusters = 3, self.init = "k-means++", self.max_iter = 300, self.tol = 1e-4, self.n_init = 10, self.verbose = 0, self.random_state = None, self.copy_x = True, self.algorithm = "auto"
| def fit(self, X, y=None, sample_weight=None): | |
| X = self._validate_data( | |
| X, | |
| accept_sparse="csr", | |
| dtype=[np.float64, np.float32], | |
| order="C", | |
| copy=self.copy_x, | |
| accept_large_sparse=False, | |
| ) | |
| self._check_params(X) | |
| random_state = check_random_state(self.random_state) | |
| sample_weight = _check_sample_weight(sample_weight, X, dtype=X.dtype) | |
| self._n_threads = _openmp_effective_n_threads() | |
| # Validate init array | |
| init = self.init | |
| if hasattr(init, "__array__"): | |
| init = check_array(init, dtype=X.dtype, copy=True, order="C") | |
| self._validate_center_shape(X, init) | |
| # subtract of mean of x for more accurate distance computations | |
| if not sp.issparse(X): | |
| X_mean = X.mean(axis=0) | |
| # The copy was already done above | |
| X -= X_mean | |
| if hasattr(init, "__array__"): | |
| init -= X_mean | |
| # precompute squared norms of data points | |
| x_squared_norms = row_norms(X, squared=True) | |
| if self._algorithm == "full": | |
| kmeans_single = _kmeans_single_lloyd | |
| self._check_mkl_vcomp(X, X.shape[0]) | |
| else: | |
| kmeans_single = _kmeans_single_elkan | |
| best_inertia, best_labels = None, None | |
| for i in range(self._n_init): | |
| # Initialize centers | |
| centers_init = self._init_centroids( | |
| X, x_squared_norms=x_squared_norms, init=init, random_state=random_state | |
| ) | |
| if self.verbose: | |
| print("Initialization complete") | |
| # run a k-means once | |
| labels, inertia, centers, n_iter_ = kmeans_single( | |
| X, | |
| sample_weight, | |
| centers_init, | |
| max_iter=self.max_iter, | |
| verbose=self.verbose, | |
| tol=self._tol, | |
| x_squared_norms=x_squared_norms, | |
| n_threads=self._n_threads, | |
| ) | |
| # determine if these results are the best so far | |
| # we chose a new run if it has a better inertia and the clustering is | |
| # different from the best so far (it's possible that the inertia is | |
| # slightly better even if the clustering is the same with potentially | |
| # permuted labels, due to rounding errors) | |
| if best_inertia is None or ( | |
| inertia < best_inertia | |
| and not _is_same_clustering(labels, best_labels, self.n_clusters) | |
| ): | |
| best_labels = labels | |
| best_centers = centers | |
| best_inertia = inertia | |
| best_n_iter = n_iter_ | |
| if not sp.issparse(X): | |
| if not self.copy_x: | |
| X += X_mean | |
| best_centers += X_mean | |
| distinct_clusters = len(set(best_labels)) | |
| if distinct_clusters < self.n_clusters: | |
| warnings.warn( | |
| "Number of distinct clusters ({}) found smaller than " | |
| "n_clusters ({}). Possibly due to duplicate points " | |
| "in X.".format(distinct_clusters, self.n_clusters), | |
| ConvergenceWarning, | |
| stacklevel=2, | |
| ) | |
| self.cluster_centers_ = best_centers | |
| self.labels_ = best_labels | |
| self.inertia_ = best_inertia | |
| self.n_iter_ = best_n_iter | |
| return self | |
| def fit_predict(self, X, y=None, sample_weight=None): | |
| """Compute cluster centers and predict cluster index for each sample. | |
| Convenience method; equivalent to calling fit(X) followed by | |
| predict(X). | |
| Parameters | |
| ---------- | |
| X : {array-like, sparse matrix} of shape (n_samples, n_features) | |
| New data to transform. | |
| y : Ignored | |
| Not used, present here for API consistency by convention. | |
| sample_weight : array-like of shape (n_samples,), default=None | |
| The weights for each observation in X. If None, all observations | |
| are assigned equal weight. | |
| Returns | |
| ------- | |
| labels : ndarray of shape (n_samples,) | |
| Index of the cluster each sample belongs to. | |
| """ | |
| return self.fit(X, sample_weight=sample_weight).labels_ | |